Vetor Definido por Dois Pontos:
Seja o vetor v ⃗ = AB ⃗ , com origem em A( x1, y1 ) e extremidade em B( x2, y2 )

Considerando os vetores OA ⃗ e OB ⃗ , onde OA ⃗ = A - 0 = ( x1, y1 ) - ( 0, 0 ) = ( x1, y1 ) e OB ⃗ = B - 0 = ( x2, y2 ) - ( 0, 0 ) = ( x2, y2 ), tem-se que OA ⃗ + AB ⃗ = OB ⃗ ou AB ⃗ = OB ⃗ - OA ⃗ = ( x2, y2 ) - ( x1, y1 ). Assim, AB ⃗ = ( x2 - x1, y2 - y1 ), o que indica que v ⃗ = AB ⃗ = B - A
Pela origem O( 0, 0 ) do sistema cartesiano ortogonal é sempre possível traçar um vetor OP ⃗ , P um ponto de coordenadas (x, y), tal que OP ⃗ tenha a mesma direção, o mesmo módulo e o mesmo sentido de AB ⃗ . Assim, o vetor OP ⃗ é equivalente ou equipolente ao vetor v ⃗ = AB ⃗ , isto é, v ⃗ = AB ⃗ = OP ⃗ , o que nos permite concluir que ( x2 - x1, y2 - y1 ) = ( x, y ).

O vetor OP ⃗ localizado na origem O ( 0, 0 ) dos eixos cartesianos é um vetor posição e, portanto, um representante do vetor, v ⃗ = AB ⃗ .
Exemplo: Dados dois pontos A ( -3, 4 ) e B( 5, -1 ), determinar o ponto P( x, y ) tal que OP ⃗ = AB ⃗ .
Solução:
OP ⃗ = P - O = ( x, y ) - ( 0, 0) = ( x, y )
AB ⃗ = B - A = ( 5, -1 ) - ( -3, 4) = ( 8, -5 )
OP ⃗ = AB ⃗ ⇒ ( x, y ) = ( 8, -5 ) ∴ P( x, y ) = P( 8, -5 )
Módulo de um Vetor:
Seja v ⃗ = OP ⃗ um vetor localizado na origem O( 0, 0 ) do sistema cartesiano ortogonal, onde P( x, y ) é a extremidade do vetor v ⃗ .
Nessa condição, o vetor v ⃗ é representado pela expressão analítica v ⃗ = ( x, y ) ou v ⃗ = xi ⃗ + yj ⃗

O módulo vetor v ⃗ , indicado por |v ⃗ |, e as componentes x e y formam um triângulo retângulo onde |v ⃗ | é a hipotenusa e x e y são os catetos. Aplicando ai o Teorema de Pitágoras, tem-se que |v ⃗ |2 = x2 + y2 ∴ |v ⃗ | = √x2 + y2.
Caso o vetor v ⃗ seja definido pelos pontos A( x1, y1 ) e B( x2, y2 ), ou seja, v ⃗ = AB ⃗ = B - A = ( x2 - x1, y2 - y1 ), então |v ⃗ | indica a distância entre os pontos A e B e será dado por |v ⃗ | = √( x2 - x1 )2 + ( y2 - y1 )2
Vetor Unitário:
Sendo unitário o vetor u ⃗ = ( x, y ), então |u ⃗ | = 1, ou seja, |u ⃗ | = √x2 + y2 = 1 ⇒ x2 + y2 = 1.
Lembrando que para todo vetor v ⃗ , v ⃗ ≠ 0, existe dois vetores unitários associados a v ⃗ , os quais são:

Ponto Médio:
Seja o segmento AB ⃗ , onde A( x1, y1 ) e B( x2, y2 ) são os seus extremos e considere M( x, y ) o ponto médio AB.

Se M é ponto médio, tem-se AM ⃗ = MB ⃗ ou M - A = B - M ⇒ M + M = A + B

Paralelismo de Vetores:
Considere os vetores u ⃗ = ( x1, y1 ) e v ⃗ = ( x2, y2 ) paralelos entre si.
Assim, u ⃗ = mv ⃗ , m ∈ R. Logo, ( x1, y1 ) = m( x2, y2 ) = ( mx2, my2 ).
Portanto, x1 = mx2 e y1 = my2 ou x1/x2 = y1/y2 = m (condição de paralelismo de dois vetores do plano).
Vetores do Espaço:
No plano R2, a base canônica é formada pelo conjunto { i ⃗ , j ⃗ }. No espaço R3, esta base passa a ser formada pelos vetores { i ⃗ , j ⃗ , k ⃗ }, onde estes vetores são unitários e ortogonais entre si, dois a dois e localizados na origem O(0, 0, 0) dos três eixos cartesianos.

i ⃗ = ( 1, 0, 0 ) localizado sobre o eixo das abscissas 0x,
j ⃗ = ( 0, 0, 1 ) sobre o eixo das ordenadas 0y.
k ⃗ = ( 0, 1, 0 ) sobre o eixo dos cotas 0z.
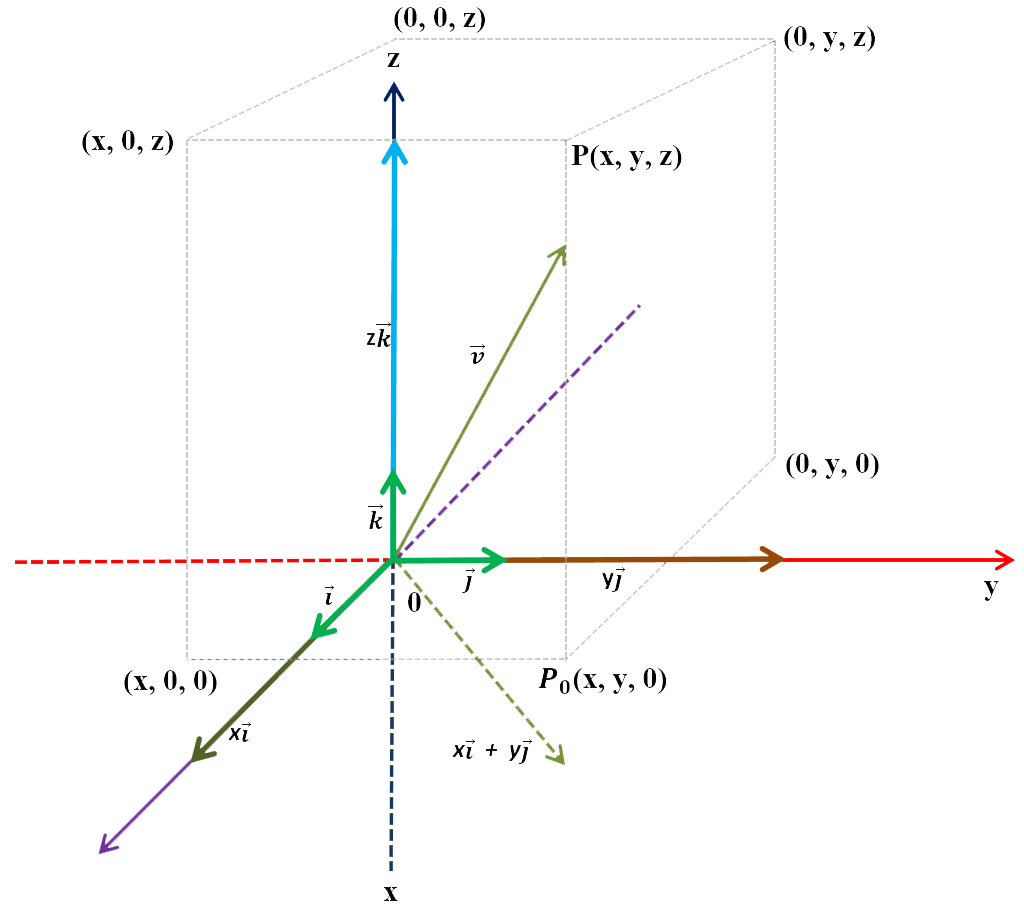
Como no plano R2, a todo ponto P( x, y,z ) do espaço R3 corresponde o vetor v ⃗ = OP ⃗ = P - O = ( x, y, z ) - ( 0, 0, 0 ) = ( x, y, z ) ∴ v ⃗ = OP ⃗ = ( x, y, z ) ou v ⃗ = OP ⃗ = xi ⃗ + yj ⃗ + zk ⃗ . Nota-se que as coordenadas do ponto extremidade P são as componentes do vetor v ⃗ = OP ⃗ .
Dados dois vetores u ⃗ = x1 i ⃗ + y1j ⃗ + z1k ⃗ e v ⃗ = x2i ⃗ + y2j ⃗ + z2k ⃗ ou u ⃗ = ( x1, y1, z1 ) e v ⃗ = ( x2, y2, z2 ), tem-se que:
1) Se u ⃗ = v ⃗ , então x1 = x2, y1 = y2 e z1 = z2
2) Se u ⃗ // v ⃗ , então u ⃗ = mv ⃗ e x1/x2 = y1/y2 = z1/z2 = m
3) |u ⃗ | = |( x1, y1, z1 )| = √( x12 + y12 + z12 ) e v ⃗ = |( x2, y2, z2 )| = √( x22 + y22 + z22 )
4) u ⃗ + v ⃗ = ( x1, y1, z1 ) + ( x2, y2, z2 ) = ( x1 + x2, y1 + y2, z1 + z2 )
5) u ⃗ - v ⃗ = ( x1, y1, z1 ) - ( x2, y2, z2 ) = ( x1 - x2, y1 - y2, z1 - z2 )
6) tv ⃗ = t( x2, y2, z2 ) = ( tx2, ty2, tz2 ), com t ∈ R, onde tv ⃗ é múltiplo escalar de vetor v ⃗ ( tv ⃗ é paralelo a v ⃗ )
Ponto Médio de um Segmento:
Aqui no espaço R3 tudo é análogo ao definido no espaço R2. Portanto, sendo A( x1, y1, z1 ) e B( x2, y2, z2 ) os pontos extremidade de um segmento AB e M( x, y, z ) o seu ponto médio, então:

Módulo do Vetor v > = ( x, y, z ):
Módulo do vetor v ⃗ = ( x, y, z ) é calculador por |v ⃗ | = |( x, y, z )| = √(x2 + y2 + z2)
De modo geral, se v ⃗ ∈ Rn, com v ⃗ = ( x1, x2, x3, ... , xn ), então:
| v | = |( x1, x2, x3, ... , xn )| = √x12 + x22 + x32+ ... + xn2