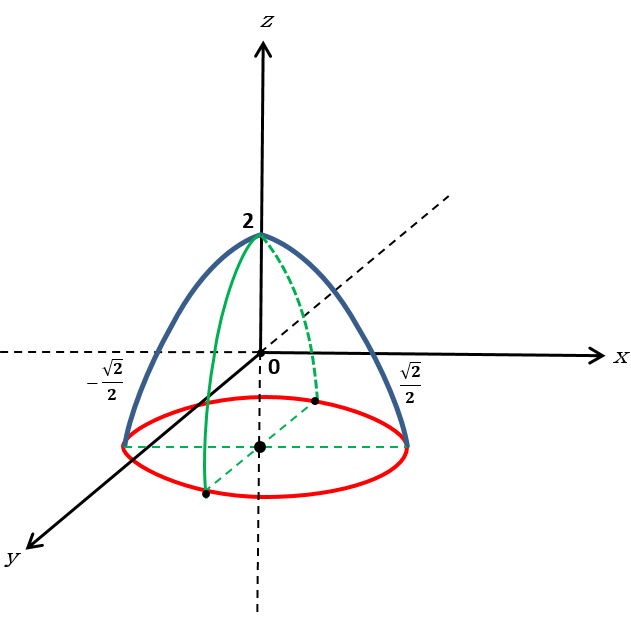
Definição

    Dá-se o nome de superfície quádrica ou simplesmente quádrica ao gráfico de uma equação do segundo grau, nas variáveis x, y e z, da forma:

    Ax² + By² + Cz² + Dxy + Exz + Fyz + Gx + Hy + Iz + K = 0, que mediante uma rotação ou translação de eixos, ou até mesmo através dos dois movimentos simultaneamente, se transforma em um dos dois tipos de equações:

    1) Ax² + By² + Cz² = D

    2) Ax² + By² + Iz = 0

Superfícies de Revolução

    é a superfície gerada pela rotação ou revolução de uma curva plana ou cônica em torno de um de seus eixos ou em torno de uma reta fixa pertencente ao plano da curva plana ou cônica.

    A reta fixa ou eixo em torno da(o) qual rotacionou a curva plana ou cônica é denominada de eixo da superfície e a curva plana ou cônica é a geratriz.

    Exemplo: Obtenha uma equação e faça o esboço do gráfico da superfície gerada pela rotação da cônica x² - 4z² = 16 e identifique a superfície em cada caso.

• em torno do eixo dos x

• em torno do eixo dos z

    Exemplo:

        x² - 4z² = 16 ou x²/16 - z²/4 = 1 é uma hipérbole, onde.

        a² = 16 e b² = 4 ⟹ a = 4 e b = 2

    Portanto, x² - 4z² = 16 é uma hipérbole de eixo transverso ou real sobre (paralelo) o eixo das abscissas (eixo dos x) e eixo conjugado ou imaginário sobre (paralelo) o eixo das cotas (eixo dos z).

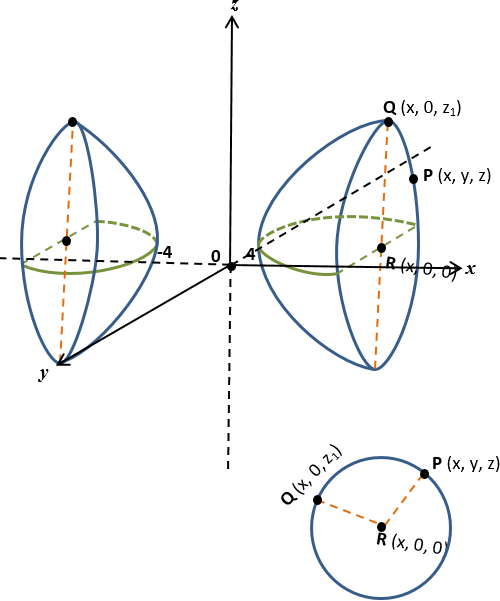
Rotação em torno do eixo dos x

    Seja Q(x, 0, z₁) um ponto pertencente à hipérbole x² - 4z² = 16

    Logo, x² - 4z₁² = 16 ⟹ x² - 16 = 4z₁² ⟹ z₁² = (x² - 16)/4 ( I )

    Ao girar a curva (hipérbole) em torno do eixo dos x, o ponto Q(x, 0, z₁) descreverá uma circunferência cujo centro é o ponto R(x, 0, 0).

    Sendo P(x, y, z) um ponto genérico dessa circunferência, tem-se que PR = QR = raio da circunferência.

    Assim, PR = √(x - x)² + (y - 0)² + (z - 0)² = √(x - x)² + (0 - 0)² + (z₁ - 0)² = QR ∴ y² + z² = z₁² (II) (I) em (II), vem:

y² + z² = (x² - 16)/4 ⟹ 4y² + 4z2 = x² - 16 ⟹ x² - 4y² - 4z² = 16

    A superfície é uma hiperboloide de revolução de 2 folhas.

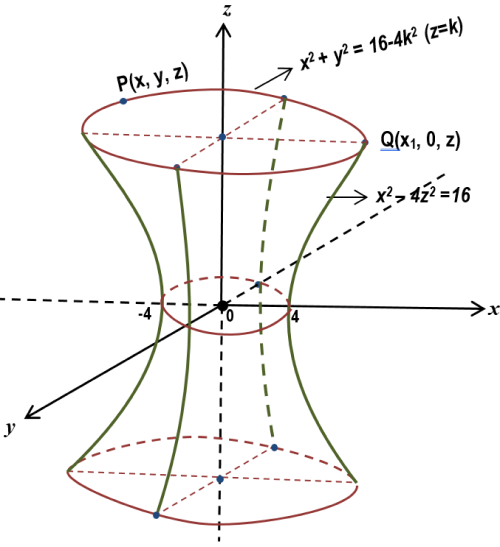
Rotação em torno do eixo dos z

    Seja Q(x₁, 0, z) um ponto pertencente à hipérbole x² - 4z² = 16.

    Logo, x₁² - 4z² = 16 ⟹ x₁² - 4z² = 16 ⟹ x₁² = 16 + 4z². (I)

    Ao girar a curva (hipérbole) em torno do eixo dos z, o ponto Q(x₁,0,z) descreverá uma circunferência cujo centro é o ponto R(0, 0, z).

    Sendo P(x, y, z) um ponto genérico dessa circunferência, tem-se que PR = QR = raio da circunferência.

PR = √(x - 0)² + (y - 0)² + (z - z)² = √(x₁ - 0)² + (0 - 0)² + (z - z)² = QR

∴ x² + y² = x₁² (II) (I) em (II), vem: x² + y² = 16 + 4z² ⟹ x² + y² - 4z² = 16 ⟹ x² + y² - 4z² = 16

    A superfície é uma hiperboloide de revolução de 1 folha.

Nota:

    Na equação de uma hiperboloide, a quantidade de sinais negativos (-) existentes na equação indica o número de folhas da superfície, ou seja: 1 sinal (-) ⟹ 1 folha; 2 sinais (-) ⟹ 2 folhas.

Hiperboloide Circular ou de Revolução

    Hiperboloide circular ou de revolução é a superfície gerada pela rotação (ou revolução) de uma hipérbole da forma x²/a² - y²/b² = 1 em torno de um de seus eixos, eixo transverso ou eixo conjugado, ou em torno de um dos eixos coordenados.

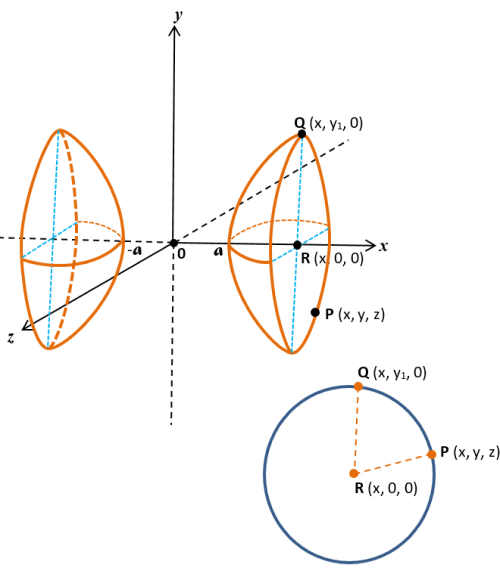
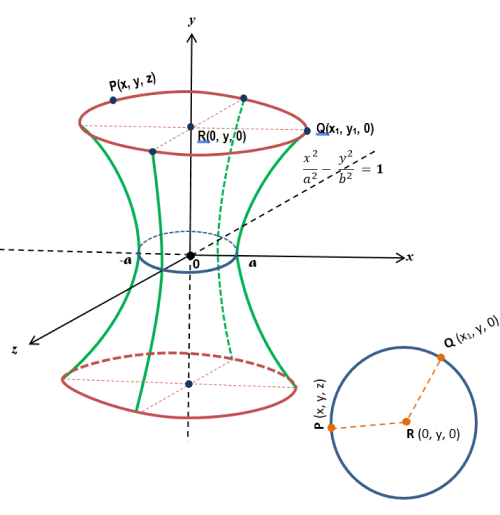
    Exemplo: Obtenha a equação e faça o esboço do gráfico da superfície gerada pela revolução da hipérbole x²/a² - y²/b² = 1 em torno do eixo das abscissas (eixo dos x).

Solução:

    Seja Q(x, y₁, 0) um ponto pertencente à hipérbole x²/a² - y²/y² = 1 . Logo, x²/a² - y₁²/b² = 1 ⟹ x²/a² - 1 = y₁²/b² ⟹ y₁² = b² (x² - a²)/a² (I).

    Ao girar a curva (hipérbole) em torno do eixo dos x, o ponto Q(x, y₁, 0) descreverá uma circunferência cujo centro é o ponto R(x, 0, 0).

    Sendo P(x, y, z) um ponto genérico dessa circunferência, tem-se que PR = QR = raio da circunferência.

PR = √(x - x)² + (y - 0)² + (z - 0)² = √(x - x)² + (y₁ - 0)² + (0 - 0)² = QR ∴ y² + z² = y₁² (II).

(I) em (II), vem: y² + z² = b² (x² - a²)/a² ⟹ y²/b² + z²/b² = x²/a² - 1 ∴ x²/a² - y²/b² - z²/b² = 1

Equação da Hiperboloide de Revolução de 2 folhas (dois sinais (-)), com eixo de rotação sobre o eixo dos x.

    OBSERVAÇÃO: A equação x²/a² - y²/b² - z²/c² = 1, com a ≠ b ≠ c, representa uma hiperboloide elíptica (não de revolução) de 2 folhas, com eixo sobre o eixo dos x.

    A equação y²/a² - x²/b² - z²/c² = 1, com a ≠ b ≠ c, representa uma hiperboloide elíptica (não de revolução) de 2 folhas, com eixo sobre o eixo dos y.

    Exemplo: Obtenha a equação e faça o esboço do gráfico da superfície gerada pela revolução da hipérbole x²/a² - y²/b² = 1 em torno do eixo das ordenadas (eixo dos y).

    Solução: Seja Q(x₁, y, 0) um ponto pertencente à hipérbole x²/a² - y²/y² = 1.

Logo, x₁²/a² - y²/b² = 1 ⟹ x₁²/a² = 1 + y²/b² ⟹ x₁² = a² (b² + y²)/b² (I).

    Ao girar a curva (hipérbole) em torno do eixo dos y, o ponto Q(x₁, y, 0) descreverá uma circunferência cujo centro é o ponto R(0, y, 0).

    Sendo P(x, y, z) um ponto genérico dessa circunferência, tem-se que PR = QR = raio da circunferência.

PR = √(x - 0)² + (y - y)² + (z - 0)² =√(x₁ - 0)² + (y - y)² + (0 - 0)² = QR ∴ x² + z² = x₁² (II).

(I) em (II), vem: x² + z² = a² (b² + y²)/b² ⟹ x²/a² + z²/a² = y²/b² + 1 ∴ x²/a² - y²/b² + z²/a² = 1.

Equação da Hiperboloide de Revolução de 1 folha (um sinal (-)), com eixo de rotação sobre o eixo dos y.

A equação x²/a² - y²/b² + z²/c² = 1, com a ≠ b ≠ c, representa uma hiperboloide elíptica (não de revolução) de 1 folha, com eixo sobre o eixo dos y.

Nota:

    Na equação da Superfície Hiperbólica, o termo com sinal diferente dos outros dois termos indica o eixo de rotação da superfície.

Elipsoide Circular ou de Revolução

    Elipsoide circular ou de revolução, é a superfície gerada pela rotação ou revolução da elipse em torno de um de seus eixos, normalmente em torno do eixo maior.

    Exemplo: Obtenha a equação e faça o esboço do gráfico da superfície gerada pela revolução da elipse x2/a² + y²/b² = 1 em torno do eixo dos x (eixo das abscissas).

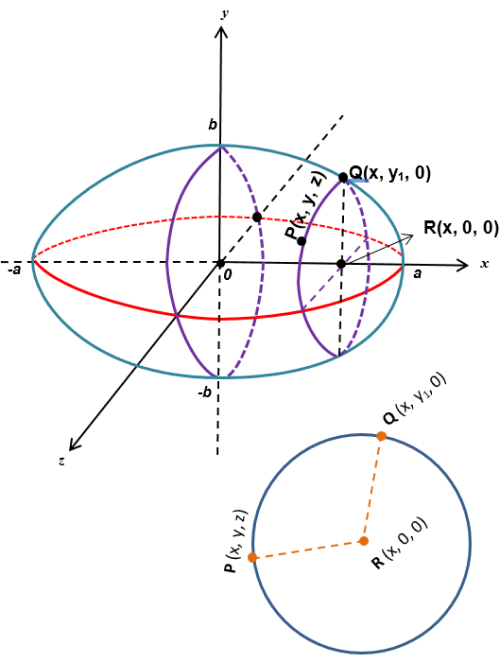
    Solução: Seja Q(x, y₁, 0) um ponto pertencente à elipse x²/a² + y²/b² = 1. Logo, x²/a² + y₁²/b² = 1 ⟹ 1 - x²/a² = y₁²/b² ⟹ y₁² = b² (a² - x²)/a² (I).

    Ao girar a curva (elipse) em torno do eixo dos x, o ponto Q(x, y₁, 0) descreverá uma circunferência cujo centro é o ponto R(x, 0, 0).

    Sendo P(x, y, z) um ponto genérico dessa circunferência, tem-se que PR = QR = raio da circunferência.

PR = √(x-x)^2+(y-0)^2 + (z - 0)² = √(x-x)^2+(y_1-0)^2+(0-0)^2 = QR ∴ y² + z² = y₁² (II).

(I) em (II), vem: y² + z² = b² ( (a² - x²)/a² ) ⟹ y²/b² + z²/b² = 1 - x²/a² ∴ x²/a² + y²/b² + z²/b² = 1.

Equação da Elipsoide de Revolução ou Circular de eixo de rotação sobre o eixo dos x.

    Nota: A equação x²/a² + y²/b² + z²/c² = 1, com a ≠ b ≠ c, representa uma elipsoide elíptica (não de revolução), com eixo sobre o eixo dos x.

    Quando a = b = c, a equação x²/a² + y²/a² + z²/a² = 1 ou x² y² + z² = a² representa uma superfície esférica.

Paraboloide circular ou de revolução

    Paraboloide circular ou de revolução é a superfície gerada pela rotação ou revolução de uma parábola em torno do seu eixo de simetria.

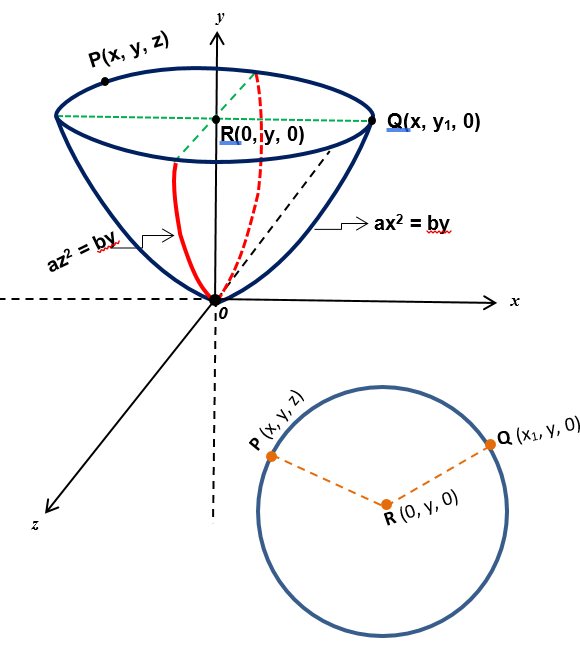
    Exemplo: Obtenha a equação e faça o esboço do gráfico da superfície gerada pela revolução da parábola ax² = by em torno do eixo dos y (eixo das ordenadas).

Solução

    Seja Q(x₁, y, 0) um ponto pertencente à parábola ax² = by.

    Logo, ax₁² = by ⟹ x₁² = by/a (I)

    Ao girar a curva (parábola) em torno do eixo dos y, o ponto Q(x₁, y, 0) descreverá uma circunferência cujo centro é o ponto R(0, y, 0).

    Sendo P(x, y, z) um ponto genérico dessa circunferência, tem-se que PR = QR = raio da circunferência.

PR = √(x - 0)² + (y - y)² + (z - 0)² = √(x₁ - 0)² + (y - y)² + (0 - 0)² = QR ∴ x² + z² = x₁² (II)

(I) em (II), vem: x² + z² = by/a ∴ ax² + az² = by.

Equação da Paraboloide de Revolução ou Circular de eixo de rotação sobre o eixo dos y.

    Nota: A equação ax² + cz² = by, com a ≠ c, representa uma paraboloide elíptica (não de revolução), com eixo sobre o eixo dos y.

Paraboloide Hiperbólico

    PARABOLOIDE HIPERBÓLICO ou SELA é a superfície ou lugar geométrico de uma equação da forma ax² - bz² = cy, com c > 0.

    A seção por um plano y = k (k > 0), é a hipérbole ax² - bz² = ck, cujos eixos transverso e conjugado são paralelos aos eixos das abscissas (eixo dos x) e das ordenadas (eixo dos y).

    A seção por um plano x = k, são parábolas de equações cy = - bz² + ak²

    A seção por um plano z = k, são parábolas de equações cy = ax² - bk²

    A seção por um plano x = 0, é a parábola de equação cy = - bz²

    A seção por um plano y = 0, é o par de retas de equações √a.x = ± √db.z

    A seção por um plano z = 0, é a parábola de equação cy = ax²

Superfície Cônica

    SUPERFÍCIE CÔNICA ou simplesmente CONE é a superfície gerada por uma reta que gira em torno de um dos eixos coordenados, passando sempre por um mesmo ponto, denominado de vértice da superfície cônica.

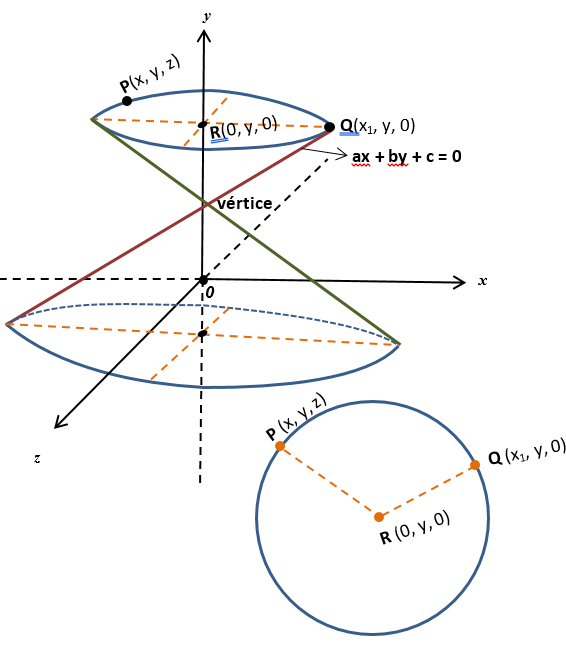
    Exemplo: Obtenha a equação e faça o esboço do gráfico da superfície gerada pela revolução da reta (r): ax + by + c = 0 em torno do eixo dos y (eixo das ordenadas).

Solução:

    Seja Q(x₁, y, 0) um ponto pertencente à reta ax + by + c = 0. Desta forma, ax₁ + by + c = 0 ⟹ x₁ = - (by + c)/a (I)

    Ao girar a curva (reta) em torno do eixo dos y, o ponto Q(x₁, y, 0) descreverá uma circunferência cujo centro é o ponto R(0, y, 0).

    Sendo P(x, y, z) um ponto genérico dessa circunferência, tem-se que PR = QR = raio da circunferência.

PR = √(x - 0)2 + (y - y)² + (z - 0)² = √(x₁ - 0)² + (y - y)² + (0 - 0)² = QR

∴ x² + z² = x₁² (II). (I) em (II), vem: x² + z² = (-(by + c)/a)²

∴ a² x² + a² z² = (by + c)² ⟹ a² x² + a² z² - (by + c)² = 0

Equação da Superfície Cônica de Revolução ou Circular

Nota:

    A equação ax² + bz² - cy² = 0, com a ≠ b, representa uma superfície cônica (ou simplesmente cone) não de revolução, ou seja, uma superfície cônica elíptica com vértice na origem O(0, 0, 0).

Superfície Cilindrica

    SUPERFÍCIE CILÍNDRICA, ou simplesmente CILINDRO, é a superfície gerada por uma reta móvel que se desloca ao longo de uma curva plana ou cônica mantendo-se paralelamente a uma reta fixa não pertencente ao plano da curva plana ou cônica. A curva plana ou cônica é denominada diretriz da superfície cilíndrica e a reta móvel é chamada de geratriz da superfície.

    Normalmente a reta fixa (e a geratriz) é perpendicular ao plano da curva plana ou cônica e, neste caso, a equação da superfície cilíndrica (ou cilindro) é a mesma equação da curva plana ou cônica.

    Exemplo: Discuta, identifique e esboce o gráfico de cada uma das superfícies seguintes:

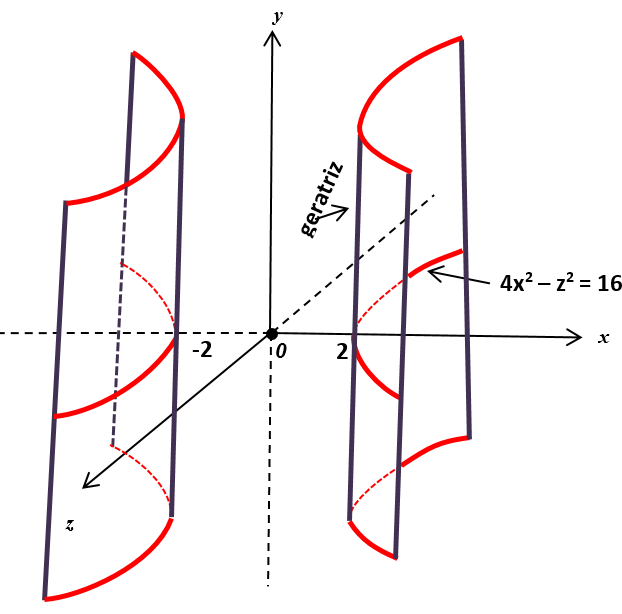
•     a) 4x2 - z² = 16

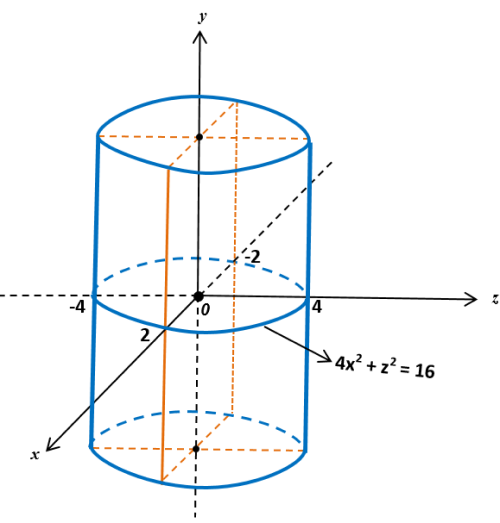
•     b) 4x² + z² = 16

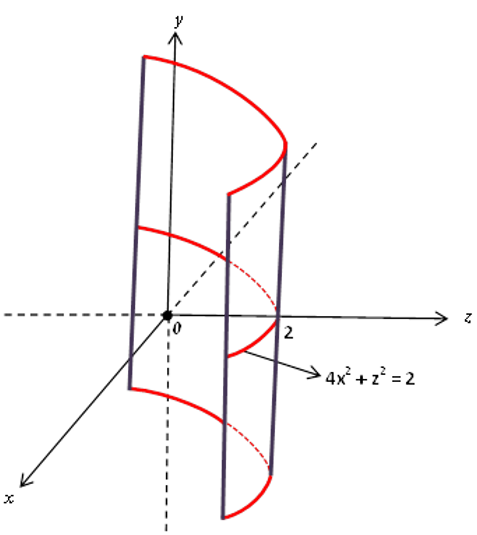
•     c) 4x²+ z = 2

•     d) 4x² + y² + z = 2

Superfície Cilíndrica hiperbólica

    Exemplo: 4x² - z² = 16 ou x²/4 - z²/16 = 1 (a² = 4 e b² = 16 ∴ a = 2 e b = 4)

    Discussão: A equação 4x² - z² = 16 representa, no plano, uma hipérbole com eixo transverso ou real sobre o eixo dos x e eixo conjugado ou imaginário sobre o eixo dos z. Portanto, no espaço, representa uma superfície cilíndrica hiperbólica, uma vez que a equação da superfície cilíndrica é a mesma equação da curva plana ou cônica (diretriz).

Superfície Cilíndrica Elíptica

Exemplo: 4x² + z² = 16 ou x²/4 + z²/16 = 1 (a² = 16 e b² = 4 ∴ a = 4 e b = 2)

    Discussão: A equação 4x² + z² = 16 representa, no plano, uma elipse com eixo maior sobre o eixo dos z e eixo menor sobre o eixo dos x. Portanto, no espaço, representa uma superfície cilíndrica elíptica (cilindro elíptico), uma vez que a equação da superfície cilíndrica é a mesma equação da curva plana ou cônica (diretriz).

Superfície cilíndrica parabólica

    Exemplo: 4x² + z = 2

    Discussão: A equação 4x² + z = 2 representa, no plano, uma parábola com eixo de simetria sobre o eixo dos z. Portanto, no espaço, representa uma superfície cilíndrica parabólica (cilindro parabólico), uma vez que a equação da superfície cilíndrica é a mesma equação da curva plana ou cônica (diretriz).

Discutindo um Exemplo de Superfície: 4x² + y² + z = 2

•     1) Se x = 0, tem-se y² + z = 2 ou z = -y² + 2, que representa uma parábola no plano y0z.

•     2) Se y = 0, tem-se 4x² + z = 2 ou z = -4x² + 2, que representa uma parábola no plano x0z.

•     3) Se z = 0, tem-se 4x² + y² = 2, que representa uma elipse no plano x0y.

•     4) Se x = k, tem-se 4k² + y² + z = 2 ou z = -y² + 2 - 4k², que representa uma parábola.

•     5) Se y = k, tem-se 4x² + k² + z = 2 ou z = -4x² + 2 - k², que representa uma parábola.

•     6) Se z = k, tem-se 4x² + y² + k = 2 ou 4x² + y² = 2 - k, que representa uma elipse, desde que 2 – k ≥ 0.

Assim, a superfície é uma parabolóide elíptica (não de revolução), com eixo sobre o eixo dos z.