Números Naturais
Subtração de números Naturais
Subtrair dois números naturais é encontrar a diferença entre
eles. Assim, a operação de subtração expressa situações que
envolvem ações de retirar, completar ou comparar.
Numa subtração temos:
| Minuendo | 485 | |
|---|---|---|
| Subtraendo | - | 179 |
| Diferença ou resto | = | 306 |
São considerados termos da subtração: o minuendo, o subtraendo e
a diferença ou resto. No conjunto dos números naturais, o
minuendo deve ser maior que o subtraendo, pois o resultado deve
ser um número positivo.
Exemplo 1
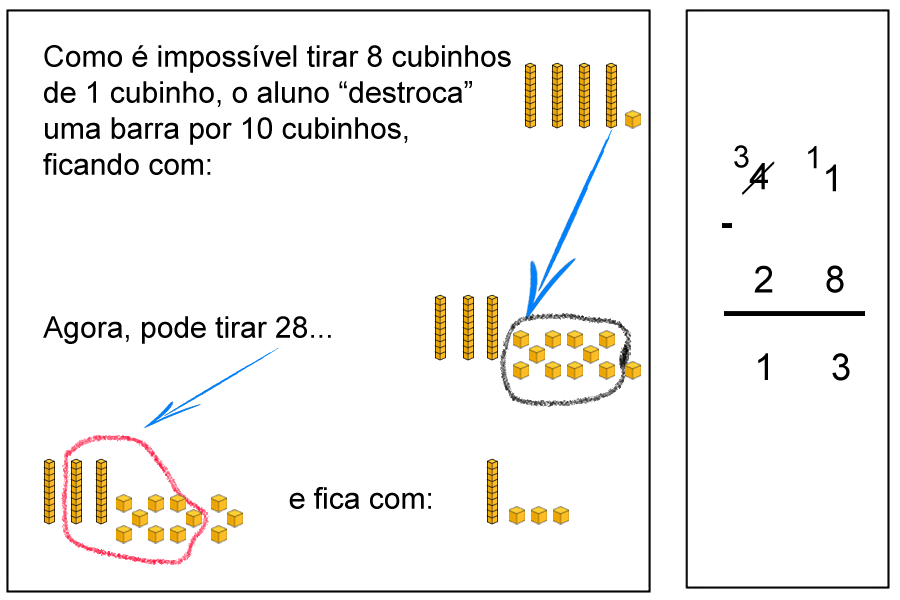
A subtração, 41 – 28 usando o material dourado
Decompõe-se os números:
41 = 40 + 1 = 4 dezenas + 1unidade
28 = 20 + 8 = 2 dezenas + 8 unidades
- Podemos subtrair dezenas;
- Não podemos subtrair unidades.
Para resolver o problema das unidades, desagrupamos uma dezena
das 4 que compõe o número e transformamos 10 unidades.
No primeiro quadro abaixo está a representação com material
dourado, e no segundo os algoritmos desta subtração.
Exemplo 2
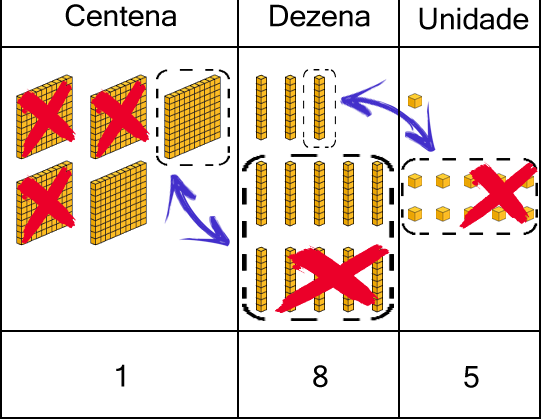
Observe a subtração: 531 – 346 usando o material dourado.
Primeiramente decompomos os números 531 e 346
531 = 500 + 30 + 1 = 5 centenas + 3 dezenas + 1 unidade
346 = 300 + 40 + 6 = 3 centenas + 4 dezenas + 6 unidades
Observe a decomposição:
- Podemos tirar 3 centenas de 5 centenas;
- Não podemos tirar 4 dezenas de 3 dezenas;
- Não podemos tirar 6 unidades de uma unidade.
Para resolver a operação vamos desagrupar transformando,
- 1 dezena em 10 unidades;
- 1 centena em 10 dezenas.
Deste modo podemos aumentar a quantidade de dezenas e unidades,
permitindo a resolução da operação. Essa ideia está na
representação abaixo fazendo uso do material dourado, no qual
também são apresentados os algoritmos da subtração.
Entender estes passos é desmistificar as ideias de “pedir
emprestado” e do “vai um”.
Exemplo 3
Resolvendo a subtração 357 – 139 =
Decompõe-se os números:
357 = 300 + 50 + 7 = 3 centenas + 5 dezenas + 7 unidades
139 = 100 + 30 + 9 = 1 centena + 3 dezenas + 9 unidades
Observe a decomposição:
- É possível subtrair centenas;
- É possível subtrair dezenas;
- Não é possível subtrair unidades.
Para resolver o problema das unidades, desagrupamos uma dezena
de 5 dezenas e transformamos em 10 unidades, que somadas as
unidades do primeiro numero, totalizam 17.
Veja na representação abaixo que após a transformação, o
primeiro número fica com 3 centenas, 4 dezenas e 17 unidades
permitindo a subtração com 139. Nesta subtração, foi realizado
apenas um desagrupamento.
| C | D | U | |
|---|---|---|---|
| 3 | 5 | 7 | |
| - | 1 | 3 | 9 |

| C | D | U | |
|---|---|---|---|
| 4 | |||
| 3 | 5 | 17 | |
| - | 1 | 3 | 9 |

| C | D | U | |
|---|---|---|---|
| 4 | |||
| 3 | 5 | 17 | |
| - | 1 | 3 | 9 |
| 2 | 1 | 8 |
Exemplo 4
Subtraindo os números 731 - 699
Decompondo os números:
731 = 700 + 30 + 1 = 7 centenas + 3 dezenas + 1
699 = 600 + 90 + 9 = 6 centenas + 9 dezenas + 9
Nesta subtração,
- Podemos subtrair centenas;
- Não é possível subtrai dezenas;
- Não é possível subtrair unidades.
Para realizar a subtração é necessário desagrupar uma dezena
para 10 unidades e uma centena para 10 dezenas.
Veja no quadro abaixo os desagrupamentos:
| C | D | U | |
|---|---|---|---|
| 7 | 3 | 1 | |
| - | 6 | 9 | 9 |

| C | D | U | |
|---|---|---|---|
| 2 | |||
| 7 | 3 | 11 | |
| - | 6 | 9 | 9 |
| 3 | 2 |

| C | D | U | |
|---|---|---|---|
| 12 | |||
| 7 | 3 | 11 | |
| - | 6 | 9 | 9 |
| 3 | 2 |

| C | D | U | |
|---|---|---|---|
| 6 | 12 | ||
| 7 | 3 | 11 | |
| - | 6 | 9 | 9 |
| 0 | 3 | 2 |